期望最大化

期望最大化 (Expectation-Maximization)

期望最大化（Expectation-maximization）算法是由 Dempster 等人 1977 年提出的统计模型参数估计的一种算法。它采用的迭代交替搜索方式可以简单有效的求解最大似然函数估计问题。已知的概率模型内部存在隐含的变量，导致了不能直接用极大似然法来估计参数，期望最大化（Expectation-maximization）就是通过迭代逼近的方式用实际的值带入求解模型内部参数的算法。它在当代的工业、商业和科学研究领域发挥了重要的作用。

期望最大化算法是一种启发式的迭代算法，是一种从 “不完全数据” 中求极大似然的方法。在人工智能、机器学习、数理统计、模式识别等许多应用都需要进行模型的参数估计，极大似然估计和极大后验似然估计是必要进行的。然而在理想的可观察变量模型中，即变量分布式均匀的时候，做出以上两个估计是显然可以的。但是实际的情况往往不是这样，某些变量并不是可以观察的，对这类模型进行极大似然估计就比较复杂了。期望最大化算法是解决对于不可观察变量进行似然估计的一种方法。期望最大化算法的提出主要是用来计算后验分布的众数或极大似然估计。然而，近年来它引起了统计学家的极大兴趣，在统计领域得到了广泛的应用。该方法广泛的应用于缺损数据、截尾数据、成群数据、带有复杂参数的数据等不完整数据。期望最大化算法流行的原因，一是在于它的理论简单化和一般性，二是许多应用都能够纳入到期望最大化算法的范畴，期望最大化算法已经成为统计学上的一个标准工具。
EM 算法还是许多非监督聚类算法的基础（如 Cheeseman et al. 1988），而且它是用于学习部分可观察马尔可夫模型（Partially Observable Markov Model）的广泛使用的 Baum-Welch 前向后向算法的基础。

给定的训练样本是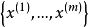，样例间独立，我们想找到每个样例隐含的类别 z，能使得 p (x,z) 最大。p (x,z) 的最大似然估计如下：

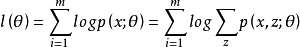
由 jensen 不等式可得：

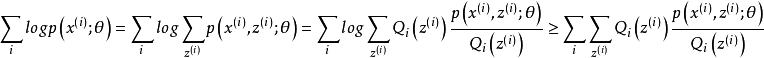
对于每一个样例 i，让表示该样例隐含变量 z 的某种分布，满足的条件是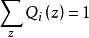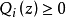，。由此，可以确定式子的下界，然后不断的提高此下界达到逼近最后真实值的目的值，这个不等式变成等式为止，然后再依据 jensen 不等式，当不等式变为等式的时候，当且仅当，也就是说 X 是常量，推出就是下面的公式：

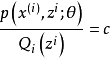
由于 Q 是随机变量 z 的概率密度函数，因此，可以得到：分子的和等于 c（分子分母都对所有 z 求和：多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是 c）。

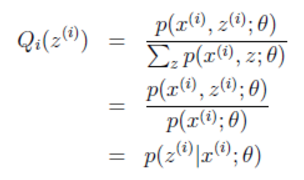
由此可得出 EM 算法的一般过程：循环重复 E 步骤和 M 步骤直到收敛。
E 步骤：对于每一个 i，计算：

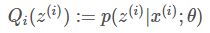
M 步骤计算:

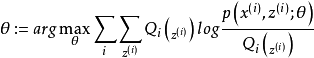
应用示例

python

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

DEBUG = True
# 调试输出函数
# 由全局变量 DEBUG 控制输出
def debug(*args, **kwargs):
    global DEBUG
    if DEBUG:
        print(*args, **kwargs)
# 第 k 个模型的高斯分布密度函数
# 每 i 行表示第 i 个样本在各模型中的出现概率
# 返回一维列表

def phi(Y, mu_k, cov_k):
    norm = multivariate_normal(mean=mu_k, cov=cov_k)
    return norm.pdf(Y)

# E 步：计算每个模型对样本的响应度
# Y 为样本矩阵，每个样本一行，只有一个特征时为列向量
# mu 为均值多维数组，每行表示一个样本各个特征的均值
# cov 为协方差矩阵的数组，alpha 为模型响应度数组
def getExpectation(Y, mu, cov, alpha):
    # 样本数
    N = Y.shape[0]
    # 模型数
    K = alpha.shape[0]

    # 为避免使用单个高斯模型或样本，导致返回结果的类型不一致
    # 因此要求样本数和模型个数必须大于1
    assert N > 1, "There must be more than one sample!"
    assert K > 1, "There must be more than one gaussian model!"

    # 响应度矩阵，行对应样本，列对应响应度
    gamma = np.mat(np.zeros((N, K)))

    # 计算各模型中所有样本出现的概率，行对应样本，列对应模型
    prob = np.zeros((N, K))
    for k in range(K):
        prob[:, k] = phi(Y, mu[k], cov[k])
    prob = np.mat(prob)

    # 计算每个模型对每个样本的响应度
    for k in range(K):
        gamma[:, k] = alpha[k] * prob[:, k]
    for i in range(N):
        gamma[i, :] /= np.sum(gamma[i, :])
    return gamma

# M 步：迭代模型参数
# Y 为样本矩阵，gamma 为响应度矩阵
def maximize(Y, gamma):
    # 样本数和特征数
    N, D = Y.shape
    # 模型数
    K = gamma.shape[1]

    #初始化参数值
    mu = np.zeros((K, D))
    cov = []
    alpha = np.zeros(K)

    # 更新每个模型的参数
    for k in range(K):
        # 第 k 个模型对所有样本的响应度之和
        Nk = np.sum(gamma[:, k])
        # 更新 mu
        # 对每个特征求均值
        for d in range(D):
            mu[k, d] = np.sum(np.multiply(gamma[:, k], Y[:, d])) / Nk
        # 更新 cov
        cov_k = np.mat(np.zeros((D, D)))
        for i in range(N):
            cov_k += gamma[i, k] * (Y[i] - mu[k]).T * (Y[i] - mu[k]) / Nk
        cov.append(cov_k)
        # 更新 alpha
        alpha[k] = Nk / N
    cov = np.array(cov)
    return mu, cov, alpha
    
# 数据预处理
# 将所有数据都缩放到 0 和 1 之间
def scale_data(Y):
    # 对每一维特征分别进行缩放
    for i in range(Y.shape[1]):
        max_ = Y[:, i].max()
        min_ = Y[:, i].min()
        Y[:, i] = (Y[:, i] - min_) / (max_ - min_)
    debug("Data scaled.")
    return Y

# 初始化模型参数
# shape 是表示样本规模的二元组，(样本数, 特征数)
# K 表示模型个数
def init_params(shape, K):
    N, D = shape
    mu = np.random.rand(K, D)
    cov = np.array([np.eye(D)] * K)
    alpha = np.array([1.0 / K] * K)
    debug("Parameters initialized.")
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha
    
# 高斯混合模型 EM 算法
# 给定样本矩阵 Y，计算模型参数
# K 为模型个数
# times 为迭代次数
def GMM_EM(Y, K, times):
    Y = scale_data(Y)
    mu, cov, alpha = init_params(Y.shape, K)
    for i in range(times):
        gamma = getExpectation(Y, mu, cov, alpha)
        mu, cov, alpha = maximize(Y, gamma)
    debug("{sep} Result {sep}".format(sep="-" * 20))
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha

python

main.py 文件：
import matplotlib.pyplot as plt
from gmm import *

# 设置调试模式
DEBUG = True

# 载入数据
Y = np.loadtxt("gmm.data")
matY = np.matrix(Y, copy=True)

# 模型个数，即聚类的类别个数
K = 2

# 计算 GMM 模型参数
mu, cov, alpha = GMM_EM(matY, K, 100)

# 根据 GMM 模型，对样本数据进行聚类，一个模型对应一个类别
N = Y.shape[0]
# 求当前模型参数下，各模型对样本的响应度矩阵
gamma = getExpectation(matY, mu, cov, alpha)
# 对每个样本，求响应度最大的模型下标，作为其类别标识
category = gamma.argmax(axis=1).flatten().tolist()[0]
# 将每个样本放入对应类别的列表中
class1 = np.array([Y[i] for i in range(N) if category[i] == 0])
class2 = np.array([Y[i] for i in range(N) if category[i] == 1])

# 绘制聚类结果
plt.plot(class1[:, 0], class1[:, 1], 'rs', label="class1")
plt.plot(class2[:, 0], class2[:, 1], 'bo', label="class2")
plt.legend(loc="best")
plt.title("GMM Clustering By EM Algorithm")
plt.show()