受限玻尔兹曼机(Restricted Boltzmann Machine)
受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)是一种可用随机神经网络(stochastic neural network)来解释的概率图模型(probabilistic graphical model)。RBM是Smolensky于1986年在波尔兹曼机(Boltzmann Machine,BM)基础上提出的,所谓“随机”是指网络中的神经元是随机神经元,输出状态只有两种(未激活和激活),状态的具体取值根据概率统计法则来决定。RBM理论是Hinton在2006年提出基于RBM的(Deep Belief Network)模型,大量学者开始研究RBM的理论及其应用。
受限玻尔兹曼机(Restricted Boltzmann Machine)是玻尔兹曼机(Boltzmann machine,BM)的一种特殊拓扑结构。BM的原理起源于统计物理学,是一种基于能量函数的建模方法,能够描述变量之间的高阶相互作用,BM的学习算法较复杂,但所建模型和学习算法有比较完备的物理解释和严格的数理统计理论作基础。
BM是一种对称耦合的随机反馈型二值单元神经网络,由可见层和多个隐层组成,网络节点分为可见单元(visible unit)和隐单元(hidden unit),用可见单元和隐单元来表达随机网络与随机环境的学习模型,通过权值表达单元之间的相关性。
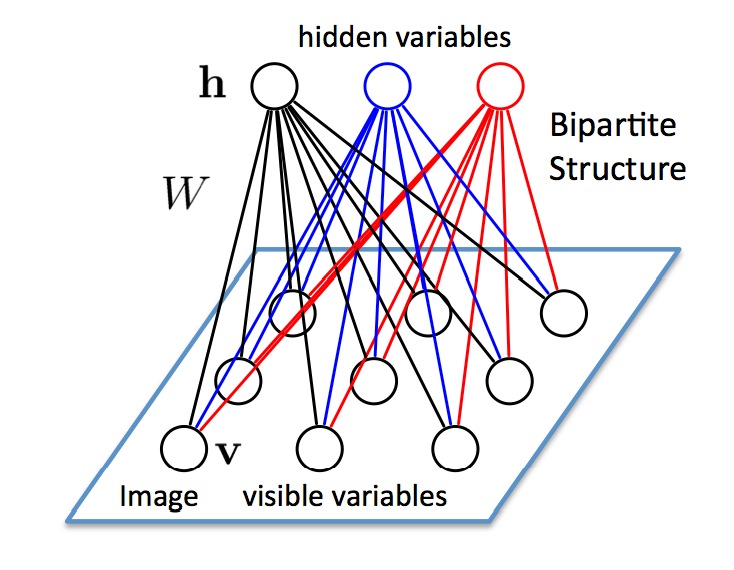
Smolensky提出的RBM由一个可见神经元层和一个隐神经元层组成,由于隐层神经元之间没有相互连接并且隐层神经元独立于给定的训练样本,这使直接计算依赖数据的期望值变得容易,可见层神经元之间也没有相互连接,通过从训练样本得到的隐层神经元状态上执行马尔可夫链抽样过程,来估计独立于数据的期望值,并行交替更新所有可见层神经元和隐层神经元的值。
受限玻兹曼机是一种玻兹曼机的变体,但限定模型必须为二分图。模型中包含对应输入参数的输入(可见)单元和对应训练结果的隐单元,图中的每条边必须连接一个可见单元和一个隐单元。(与此相对,“无限制”玻兹曼机包含隐单元间的边,使之成为递归神经网络。)这一限定使得相比一般玻兹曼机更高效的训练算法成为可能,特别是基于梯度的对比分歧(contrastive divergence)算法。
受限玻兹曼机也可被用于深度学习网络。具体地,深度信念网络可使用多个RBM堆叠而成,并可使用梯度下降法和反向传播算法进行调优
RBM是有两个层的浅层神经网络,它是组成深度置信网络的基础部件。RBM的第一个层称为可见层,又称输入层,而第二个层是隐藏层。
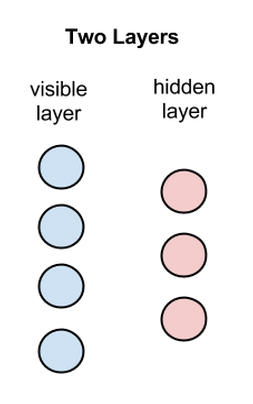
图中每个圆圈都是一个与神经元相似的单元,称为节点,运算在节点中进行。一个层中的节点与另一层中的所有节点分别连接,但与同一层中的其他节点并不相连。
也就是说,层的内部不存在通信-这就是受限玻尔兹曼机被称为受限的原因。每个节点对输入进行处理和运算,判定是否继续传输输入的数据,而这种判定一开始是随机的。(“随机”(stochastic)一词在此处指与输入相乘的初始系数是随机生成的。)
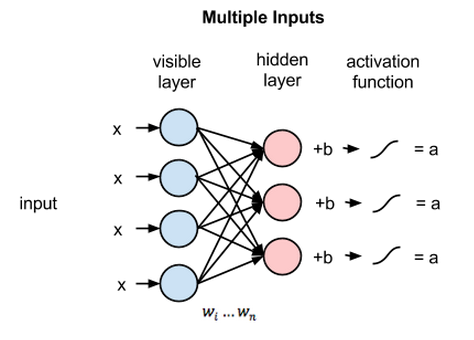
每个可见节点负责处理网络需要学习的数据集中一个项目的一种低层次特征。举例来说,如果处理的是一个灰度图像的数据集,则每个可见节点将接收一张图像中每个像素的像素值。(MNIST图像有784个像素,所以处理这类图像的神经网络的一个可见层必须有784个输入节点。)
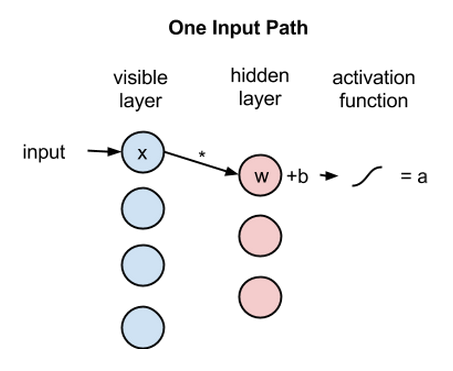
接着来看单个像素值x如何通过这一双层网络。在隐藏层的节点1中x与一个权重相乘,再与所谓的偏差相加。这两步运算的结果输入激活函数,得到节点的输出,即输入为x时通过节点的信号强度。
激活函数f((权重w * 输入x) + 偏差b ) = 输出a
|
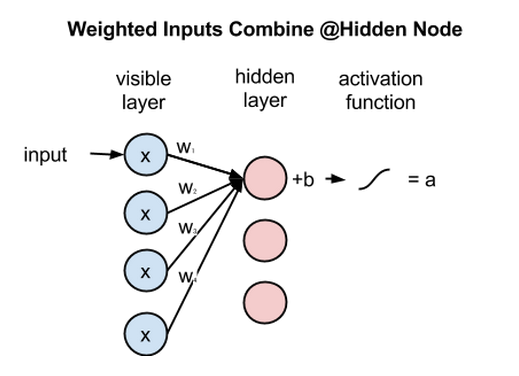
一个隐藏节点如何整合多项输入。每个x分别与各自的权重相乘,乘积之和再与偏差相加,其结果同样经过激活函数运算得到节点的输出值。
由于每个可见节点的输入都被传递至所有的隐藏节点,所以也可将RBM定义为一种对称二分图。
对称指每个可见节点都与所有的隐藏节点相连接(见下图)。二分指有两个部分或层,而这里的图是指代节点网络的数学名词。
在每个隐藏节点中,每一个输入x都会与其相对应的权重w相乘。也就是说,每个输入x会对应三个权重,因此总共有12个权重(4个输入节点 x 3个隐藏节点)。两层之间的权重始终都是一个行数等于输入节点数、列数等于输出节点数的矩阵。
每个隐藏节点会接收四个与对应权重相乘后的输入值。这些乘积之和与一个偏差值相加(至少能强制让一部分节点激活),其结果再经过激活运算得到每个隐藏节点的输出a。
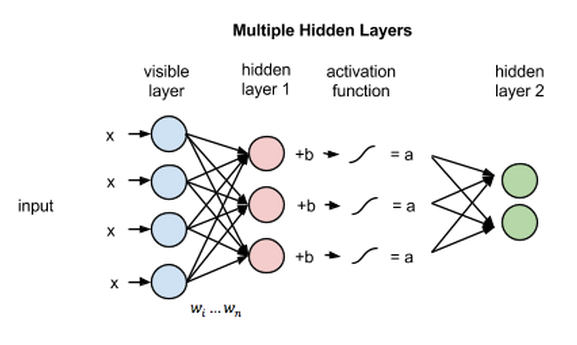
如果这两个层属于一个深度神经网络,那么第一隐藏层的输出会成为第二隐藏层的输入,随后再通过任意数量的隐藏层,直至到达最终的分类层。(简单的前馈动作仅能让RBM节点实现自动编码器的功能。)
在重构阶段,第一隐藏层的激活值成为反向传递中的输入。这些输入值与同样的权重相乘,每两个相连的节点之间各有一个权重,就像正向传递中输入x的加权运算一样。这些乘积的和再与每个可见层的偏差相加,所得结果就是重构值,亦即原始输入的近似值。这一过程表示如下:
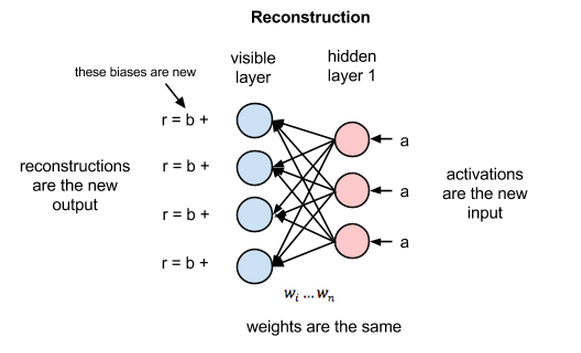
由于RBM权重初始值是随机决定的,重构值与原始输入之间的差别通常很大。可以将r值与输入值之差视为重构误差,此误差值随后经由反向传播来修正RBM的权重,如此不断反复,直至误差达到最小。
由此可见,RBM在正向传递中使用输入值来预测节点的激活值,亦即输入为加权的x时输出的概率:p(a|x; w)。
但在反向传递时,激活值成为输入,而输出的是对于原始数据的重构值,或者说猜测值。此时RBM则是在尝试估计激活值为a时输入为x的概率,激活值的加权系数与正向传递中的权重相同。 第二个阶段可以表示为p(x|a; w)。
上述两种预测值相结合,可以得到输入 x 和激活值 a 的联合概率分布,即p(x, a)。
重构与回归、分类运算不同。回归运算根据许多输入值估测一个连续值,分类运算是猜测应当为一个特定的输入样例添加哪种具体的标签。
而重构则是在猜测原始输入的概率分布,亦即同时预测许多不同的点的值。这被称为生成学习,必须和分类器所进行的判别学习区分开来,后者是将输入值映射至标签,用直线将数据点划分为不同的组。
试想输入数据和重构数据是形状不同的常态曲线,两者仅有部分重叠。
KL散度衡量两条曲线下方不重叠(即离散)的面积,而RBM的优化算法会尝试将这些离散部分的面积最小化,使共用权重在与第一隐藏层的激活值相乘后,可以得到与原始输入高度近似的结果。下图左半边是一组原始输入的概率分布曲线p,与之并列的是重构值的概率分布曲线q;右半边的图则显示了两条曲线之间的差异。
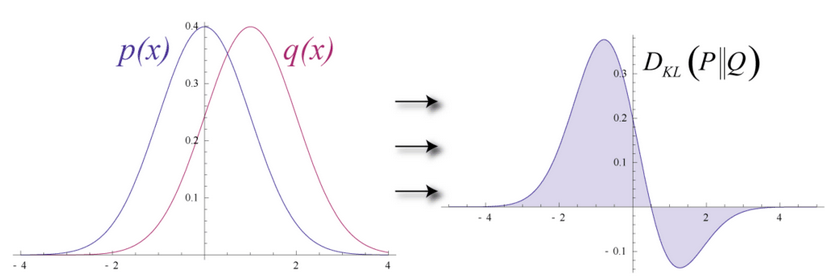
RBM根据权重产生的误差反复调整权重,以此学习估计原始数据的近似值。可以说权重会慢慢开始反映出输入的结构,而这种结构被编码为第一个隐藏层的激活值。整个学习过程看上去像是两条概率分布曲线在逐步重合。
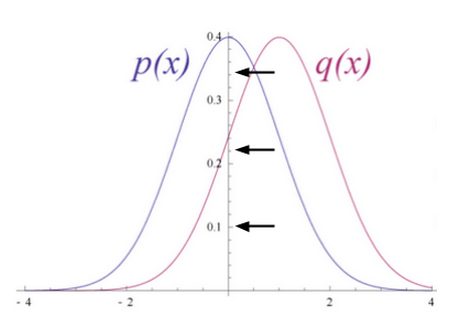
RBM根据第一个隐藏层的激活值学习了输入数据的结构之后,数据即在网络中继续向下传递一层。第一个隐藏层的作用现在相当于可见层。激活值实际上相当于输入,在第二个隐藏层的节点中与权重相乘,得到另一组激活值。
将特征分组,再将特征组分组,由此连续生成多组激活值的过程是特征层次分析的基础,神经网络用这种方法来学习更为复杂且抽象的数据表达形式。
每增加一个隐藏层,其权重都会反复进行调整,直到该层能较为准确地模拟出来自前一层的输入。这是无监督的逐层贪婪预训练方法,不需要标签就可以改进网络的权重,也就是说可以采用未标记、未经人工处理的数据来训练,而现实中大部分的数据都属于这一类别。一般的规律是,算法接触的数据越多,产生的结果越准确,这正是深度学习算法十分厉害的原因之一。
权重能够近似模拟出数据的特征后,也就为下一步的学习奠定了良好基础,比如可以在随后的有监督学习阶段使用深度置信网络来对图像进行分类。
RBM有许多用途,其中最强的功能之一就是对权重进行合理的初始化,为之后的学习和分类做好准备。从某种意义上来说,RBM的作用与反向传播相似:让权重能够有效地模拟数据。可以认为预训练和反向传播是实现同一个目的的不同方法,二者可以相互替代。
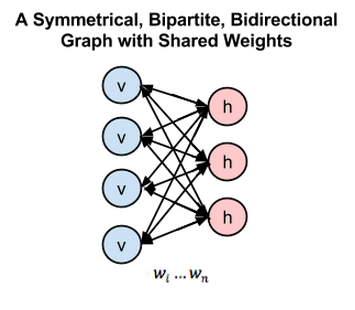
这幅对称二分二向图综合显示了玻尔兹曼机的运作方式。
应用示例
import tensorflow as tf
import numpy as np
import sys
from .util import tf_xavier_init
class RBM:
def __init__(self,
n_visible,
n_hidden,
learning_rate=0.01,
momentum=0.95,
xavier_const=1.0,
err_function='mse',
use_tqdm=False,
tqdm=None):
if not 0.0 <= momentum <= 1.0:
raise ValueError('momentum should be in range [0, 1]')
if err_function not in {'mse', 'cosine'}:
raise ValueError('err_function should be either \'mse\' or \'cosine\'')
self._use_tqdm = use_tqdm
self._tqdm = None
if use_tqdm or tqdm is not None:
from tqdm import tqdm
self._tqdm = tqdm
self.n_visible = n_visible
self.n_hidden = n_hidden
self.learning_rate = learning_rate
self.momentum = momentum
self.x = tf.placeholder(tf.float32, [None, self.n_visible])
self.y = tf.placeholder(tf.float32, [None, self.n_hidden])
self.w = tf.Variable(tf_xavier_init(self.n_visible, self.n_hidden, const=xavier_const), dtype=tf.float32)
self.visible_bias = tf.Variable(tf.zeros([self.n_visible]), dtype=tf.float32)
self.hidden_bias = tf.Variable(tf.zeros([self.n_hidden]), dtype=tf.float32)
self.delta_w = tf.Variable(tf.zeros([self.n_visible, self.n_hidden]), dtype=tf.float32)
self.delta_visible_bias = tf.Variable(tf.zeros([self.n_visible]), dtype=tf.float32)
self.delta_hidden_bias = tf.Variable(tf.zeros([self.n_hidden]), dtype=tf.float32)
self.update_weights = None
self.update_deltas = None
self.compute_hidden = None
self.compute_visible = None
self.compute_visible_from_hidden = None
self._initialize_vars()
assert self.update_weights is not None
assert self.update_deltas is not None
assert self.compute_hidden is not None
assert self.compute_visible is not None
assert self.compute_visible_from_hidden is not None
if err_function == 'cosine':
x1_norm = tf.nn.l2_normalize(self.x, 1)
x2_norm = tf.nn.l2_normalize(self.compute_visible, 1)
cos_val = tf.reduce_mean(tf.reduce_sum(tf.mul(x1_norm, x2_norm), 1))
self.compute_err = tf.acos(cos_val) / tf.constant(np.pi)
else:
self.compute_err = tf.reduce_mean(tf.square(self.x - self.compute_visible))
init = tf.global_variables_initializer()
self.sess = tf.Session()
self.sess.run(init)
def _initialize_vars(self):
pass
def get_err(self, batch_x):
return self.sess.run(self.compute_err, feed_dict={self.x: batch_x})
def get_free_energy(self):
pass
def transform(self, batch_x):
return self.sess.run(self.compute_hidden, feed_dict={self.x: batch_x})
def transform_inv(self, batch_y):
return self.sess.run(self.compute_visible_from_hidden, feed_dict={self.y: batch_y})
def reconstruct(self, batch_x):
return self.sess.run(self.compute_visible, feed_dict={self.x: batch_x})
def partial_fit(self, batch_x):
self.sess.run(self.update_weights + self.update_deltas, feed_dict={self.x: batch_x})
def fit(self,
data_x,
n_epoches=10,
batch_size=10,
shuffle=True,
verbose=True):
assert n_epoches > 0
n_data = data_x.shape[0]
if batch_size > 0:
n_batches = n_data // batch_size + (0 if n_data % batch_size == 0 else 1)
else:
n_batches = 1
if shuffle:
data_x_cpy = data_x.copy()
inds = np.arange(n_data)
else:
data_x_cpy = data_x
errs = []
for e in range(n_epoches):
if verbose and not self._use_tqdm:
print('Epoch: {:d}'.format(e))
epoch_errs = np.zeros((n_batches,))
epoch_errs_ptr = 0
if shuffle:
np.random.shuffle(inds)
data_x_cpy = data_x_cpy[inds]
r_batches = range(n_batches)
if verbose and self._use_tqdm:
r_batches = self._tqdm(r_batches, desc='Epoch: {:d}'.format(e), ascii=True, file=sys.stdout)
for b in r_batches:
batch_x = data_x_cpy[b * batch_size:(b + 1) * batch_size]
self.partial_fit(batch_x)
batch_err = self.get_err(batch_x)
epoch_errs[epoch_errs_ptr] = batch_err
epoch_errs_ptr += 1
if verbose:
err_mean = epoch_errs.mean()
if self._use_tqdm:
self._tqdm.write('Train error: {:.4f}'.format(err_mean))
self._tqdm.write('')
else:
print('Train error: {:.4f}'.format(err_mean))
print('')
sys.stdout.flush()
errs = np.hstack([errs, epoch_errs])
return errs
def get_weights(self):
return self.sess.run(self.w),\
self.sess.run(self.visible_bias),\
self.sess.run(self.hidden_bias)
def save_weights(self, filename, name):
saver = tf.train.Saver({name + '_w': self.w,
name + '_v': self.visible_bias,
name + '_h': self.hidden_bias})
return saver.save(self.sess, filename)
def set_weights(self, w, visible_bias, hidden_bias):
self.sess.run(self.w.assign(w))
self.sess.run(self.visible_bias.assign(visible_bias))
self.sess.run(self.hidden_bias.assign(hidden_bias))
def load_weights(self, filename, name):
saver = tf.train.Saver({name + '_w': self.w,
name + '_v': self.visible_bias,
name + '_h': self.hidden_bias})
saver.restore(self.sess, filename)
|
原文:https://github.com/KeKe-Li/tutorial





















