等度量映射(IsometricMapping,Isomap)

等度量映射(Isomap)是最经典的非线性映射降维方法之一，它在MDS的基础上引入了“测地距离”的概念，直接解决了MDS使用欧氏距离无法应对非线性流形的问题。测地距离(Geometric Distance)是高维流形中两点之间的最短距离，高维流形中，空间是不规则的，所以最短距离不一定是直线距离(欧氏距离)。就像蚂蚁从立方体的一面爬到另一面，不能直接横穿立方体一样。

图中左边的两个点的最近距离是蓝色实线的距离，而不应该是虚线的距离。

通常情况下真实的测地距离是非常难以求出的，但是等度量映射基于流形局部近似于欧式空间的定义提出了一种近似的求解方式。

我们通常的做法是:

  1. 求得原样本的KNN图，并依据定义保留其欧式距离。

  2. 所有非KNN的点间的距离规定为无穷大。

  3. 用dijkstra或floyd求出任意两点的最短路便可近似表示两点间的测地距离。

  4. 然后等度量映射(Isomap)将得到的测地距离矩阵输入MDS完成降维。

最后等度量映射(Isomap)将得到的测地距离矩阵输入MDS完成降维。

最后的结果是这样的。

应用示例:

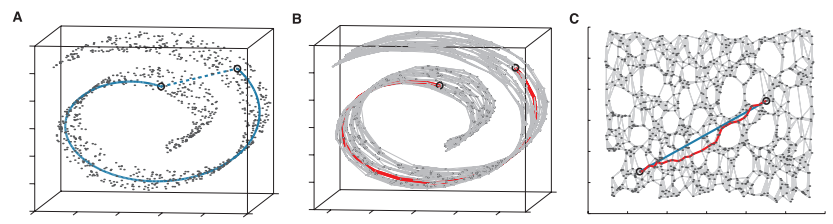
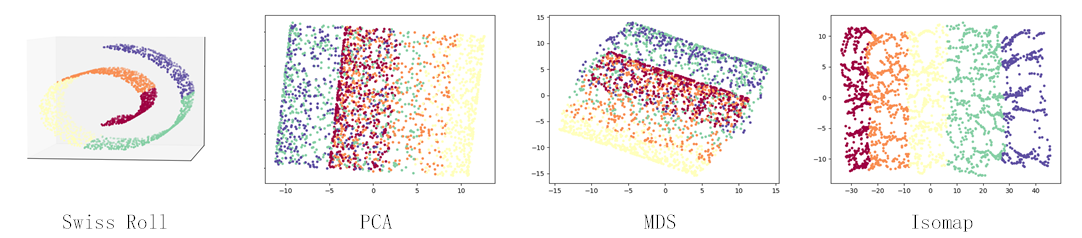
from IsomapCuda import *
from DataUtils import *
import getopt,sys

GPU_MEM_SIZE = 512

def Isomap(dataSet,outfile,srcDims,trgDims,k,eps=1000000000., CIsomap=False):
    """
    Classical isomap
    """
    
    #first do KNN
    knnRefs,knnDists,knnm = KNN(dataSet,k,eps,srcDims)
    mdists = []
    if CIsomap:
        mdists = C_Isomap(knnDists,knnm,k)
    
    #then do APSP
    pathMatrix = APSP(knnRefs,knnDists,knnm,eps)
    del knnRefs
    del knnDists
    del knnm
    
    #then normalize the matrix
    normMatrix = NormMatrix(pathMatrix,mdists)
    del pathMatrix
    del mdists
    
    #then get eigenvalues
    #embedding = EigenEmbedding(normMatrix,trgDims)
    embedding = QEig(normMatrix,trgDims)
    del normMatrix
    
    return embedding


def NMIsomap(dataSet,outfile,srcDims,trgDims,k,eps=1000000000., saveSteps = False):
    """
    Non-Metric Isomap
    """
    
    #first do KNN
    knnRefs,knnDists = loadSplitTable(KNN(dataSet,k,eps,srcDims))
    
    #then do APSP
    pathMatrix = APSP(knnRefs,knnDists,eps)
    del knnRefs
    del knnDists
    
    #XXX:hacky way of saving this info
    if saveSteps:
        saveTable(pathMatrix,outfile[:-4]+'_distances.csv')
    
    #then get the rank matrix
    origDims = len(pathMatrix)
    rankMatrix = RankMatrix(pathMatrix)
    del pathMatrix
    
    #then get the NMDS embedding
    embedding = NMDS(rankMatrix, loadMatrix(dataSet)[:,:trgDims], origDims, trgDims)
    
    return embedding



if __name__ == '__main__':
    arg_values = ['nonmetric=','outdims=','indims=','if=','of=','k=','eps=','help','h']
    optlist, args = getopt.getopt(sys.argv[1:], 'x', arg_values)
    
    trgDims = 3
    srcDims = 10000000000
    k =6
    eps = 1000000000.
    infile='swissroll.csv'
    outfile='embedding.csv'
    nonmetric=False
    
    
    for o in optlist:
        if o[0].strip('-') == 'outdims':
            trgDims = int(o[1])
    for o in optlist:
        if o[0].strip('-') == 'indims':
            srcDims = int(o[1])
    for o in optlist:
        if o[0].strip('-') == 'if':
            infile = o[1]
    for o in optlist:
        if o[0].strip('-') == 'of':
            outfile = o[1]
    for o in optlist:
        if o[0].strip('-') == 'k':
            k = int(o[1])
    for o in optlist:
        if o[0].strip('-') == 'nonmetric':
            if o[1].strip(' \r\n\t') == 'True' or o[1].strip(' \r\n\t') == 'true':
                nonmetric = True
        
    for o in optlist:
        if o[0].strip('-') == 'help' or o[1].strip('-') == 'h':
            print "The following commands are available:"
            print "\t--if=inputfile\tDefaults to swissroll.csv"
            print "\t--of=outputfile\tDefaults to embedding.csv"
            print "\t--k=k_nearest_neighbours\tDefaults to 12"
            print "\t--outdims=embedding_dimensions\tDefaults to 3"
            print "\t--indims=input_dimensions\tDefaults to all in the input file"
            print "\t--nonmetric\tEnables non-metric MDS embeddings"
    result = None
    if not nonmetric:
        result = Isomap(infile,outfile,srcDims,trgDims,k,eps,False)
    else:
        result = NMIsomap(infile,outfile,srcDims,trgDims,k,eps,False)
    
    saveTable(result,outfile)

原文：https://github.com/KeKe-Li/tutorial