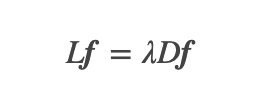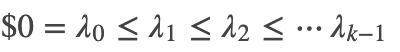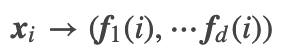from numpy import exp, median
from scipy.sparse.csgraph import laplacian
from sklearn.manifold.locally_linear import (
null_space, LocallyLinearEmbedding)
from sklearn.metrics.pairwise import pairwise_distances, rbf_kernel
from sklearn.neighbors import kneighbors_graph, NearestNeighbors
def ler(X, Y, n_components=2, affinity='nearest_neighbors',
n_neighbors=None, gamma=None, mu=1.0, y_gamma=None,
eigen_solver='auto', tol=1e-6, max_iter=100,
random_state=None):
"""
Laplacian Eigenmaps for Regression (LER)
Parameters
----------
X : ndarray, 2-dimensional
The data matrix, shape (num_points, num_dims)
Y : ndarray, 1 or 2-dimensional
The response matrix, shape (num_points, num_responses).
n_components : int
Number of dimensions for embedding. Default is 2.
affinity : string or callable, default : "nearest_neighbors"
How to construct the affinity matrix.
- 'nearest_neighbors' : construct affinity matrix by knn graph
- 'rbf' : construct affinity matrix by rbf kernel
n_neighbors : int, optional, default=None
Number of neighbors for kNN graph construction on X.
gamma : float, optional, default=None
Scaling factor for RBF kernel on X.
mu : float, optional, default=1.0
Influence of the Y-similarity penalty.
y_gamma : float, optional
Scaling factor for RBF kernel on Y.
Defaults to the inverse of the median distance between rows of Y.
Returns
-------
embedding : ndarray, 2-dimensional
The embedding of X, shape (num_points, n_components)
"""
if eigen_solver not in ('auto', 'arpack', 'dense'):
raise ValueError("unrecognized eigen_solver '%s'" % eigen_solver)
nbrs = NearestNeighbors(n_neighbors=n_neighbors + 1)
nbrs.fit(X)
X = nbrs._fit_X
Nx, d_in = X.shape
Ny = Y.shape[0]
if n_components > d_in:
raise ValueError("output dimension must be less than or equal "
"to input dimension")
if Nx != Ny:
raise ValueError("X and Y must have same number of points")
if affinity == 'nearest_neighbors':
if n_neighbors >= Nx:
raise ValueError("n_neighbors must be less than number of points")
if n_neighbors == None or n_neighbors <= 0:
raise ValueError("n_neighbors must be positive")
elif affinity == 'rbf':
if gamma != None and gamma <= 0:
raise ValueError("n_neighbors must be positive")
else:
raise ValueError("affinity must be 'nearest_neighbors' or 'rbf' must be positive")
if Y.ndim == 1:
Y = Y[:, None]
if y_gamma is None:
dists = pairwise_distances(Y)
y_gamma = 1.0 / median(dists)
if affinity == 'nearest_neighbors':
affinity = kneighbors_graph(X, n_neighbors, include_self=True)
else:
if gamma == None:
dists = pairwise_distances(X)
gamma = 1.0 / median(dists)
affinity = kneighbors_graph(X, n_neighbors, mode='distance', include_self=True)
affinity.data = exp(-gamma * affinity.data ** 2)
K = rbf_kernel(Y, gamma=y_gamma)
lap = laplacian(affinity, normed=True)
lapK = laplacian(K, normed=True)
embedding, _ = null_space(lap + mu * lapK, n_components,
k_skip=1, eigen_solver=eigen_solver,
tol=tol, max_iter=max_iter,
random_state=random_state)
return embedding
class LER(LocallyLinearEmbedding):
"""Scikit-learn compatible class for LER."""
def __init__(self, n_components=2, affinity='nearest_neighbors',
n_neighbors=2, gamma=None, mu=1.0, y_gamma=None,
eigen_solver='auto', tol=1E-6, max_iter=100,
random_state=None, neighbors_algorithm='auto'):
self.n_components = n_components
self.affinity = affinity
self.n_neighbors = n_neighbors
self.gamma = gamma
self.mu = mu
self.y_gamma = y_gamma
self.eigen_solver = eigen_solver
self.tol = tol
self.max_iter = max_iter
self.random_state = random_state
self.neighbors_algorithm = neighbors_algorithm
def fit_transform(self, X, Y):
self.fit(X, Y)
return self.embedding_
def fit(self, X, Y):
self.nbrs_ = NearestNeighbors(self.n_neighbors,
algorithm=self.neighbors_algorithm)
self.nbrs_.fit(X)
self.embedding_ = ler(
X, Y, n_components=self.n_components,
affinity=self.affinity, n_neighbors=self.n_neighbors,
gamma=self.gamma, mu=self.mu, y_gamma=self.y_gamma,
eigen_solver=self.eigen_solver, tol=self.tol,
max_iter=self.max_iter, random_state=self.random_state)
return self
|
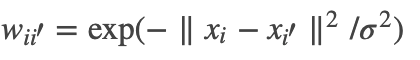；而对其它点对权值赋0. 最终我们可以用邻接矩阵W来表示这个图.
wechat
alipay
