递归神经网络
递归神经网络(Recurrent Neural Network)
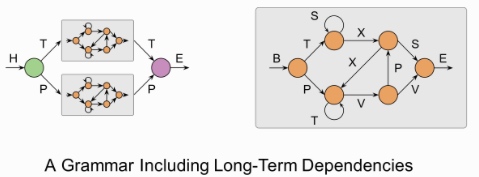
递归神经网络(Recurrent neural networks,简称RNN)是一种通过隐藏层节点周期性的连接,来捕捉序列化数据中动态信息的神经网络,可以对序列化的数据进行分类。和其他前向神经网络不同,RNN可以保存一种上下文的状态,甚至能够在任意长的上下文窗口中存储、学习、表达相关信息,而且不再局限于传统神经网络在空间上的边界,可以在时间序列上有延拓,直观上讲,就是本时间的隐藏层和下一时刻的隐藏层之间的节点间有边。
RNN广泛应用在和序列有关的场景,如如一帧帧图像组成的视频,一个个片段组成的音频,和一个个词汇组成的句子。尽管RNN有一些传统的缺点,如难以训练,参数较多,但近些年来关于网络结构、优化手段和并行计算的深入研究使得大规模学习算法成为可能,尤其是LSTM与BRNN算法的成熟,使得图像标注、手写识别、机器翻译等应用取得了突破性进展。
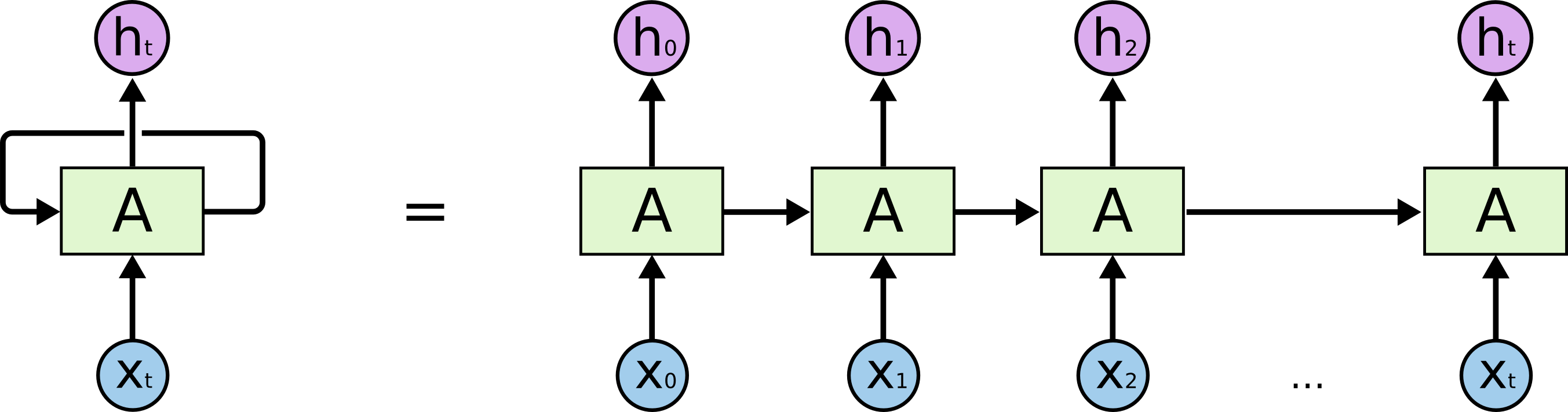
RNN主要解决序列数据的处理,比如文本、语音、视频等等。这类数据的样本间存在顺序关系,每个样本和它之前的样本存在关联。比如说,在文本中,一个词和它前面的词是有关联的;在气象数据中,一天的气温和前几天的气温是有关联的。一组观察数据定义为一个序列,从分布中可以观察出多个序列。
一个序列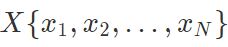 的最简单模型为
的最简单模型为
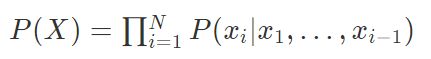
当然,这个模型存在致命的问题:它的复杂度会爆炸性增长,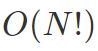 隐马尔科夫模型(HMM)定义每个元素只和离它最近的kk个元素相关,解决了复杂度暴增的问题,模型为:
隐马尔科夫模型(HMM)定义每个元素只和离它最近的kk个元素相关,解决了复杂度暴增的问题,模型为:
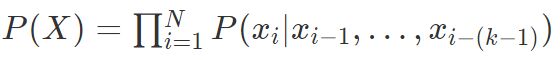
当k=1时,模型变为:
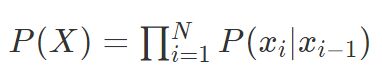
只考虑观察值X的模型有时表现力不足,因此需要加入隐变量,将观察值建模成由隐变量所生成。隐变量的好处在于,它的数量可以比观察值多,取值范围可以比观察值更广,能够更好的表达有限的观察值背后的复杂分布。加入了隐变量hh的马尔科夫模型称为隐马尔科夫模型。
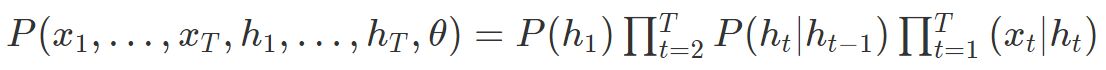
隐马尔科夫模型实际上建模的是观察值X,隐变量h和模型参数θ的联合分布,HMM的模型长度T是事先固定的,模型参数不共享,其复杂度为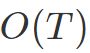 。
。
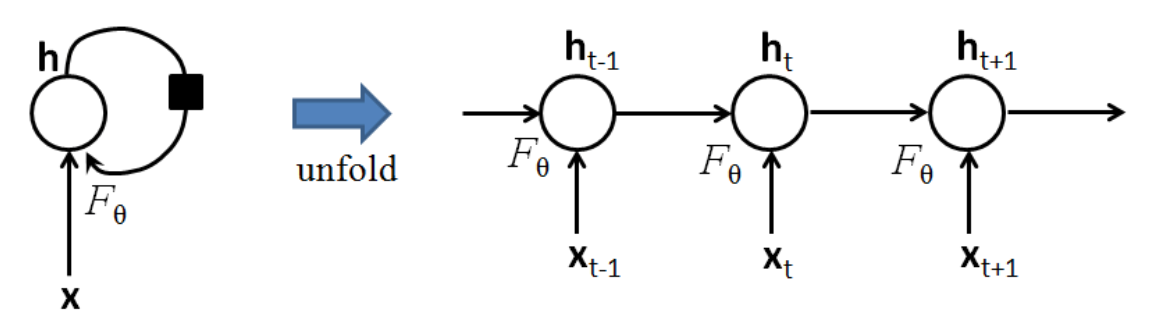
把序列视作时间序列,隐含层h的自连接边实际上是和上一时刻的h相连.在每一个时刻t,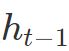 的取值是当前时刻的输入
的取值是当前时刻的输入![]() ,和上一时刻的隐含层值
,和上一时刻的隐含层值![]() 的一个函数:
的一个函数:
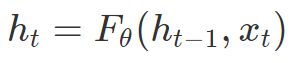
将h层的自连接展开,就成为了上图右边的样子,看上去和HMM很像。两者最大的区别在于,RNN的参数是跨时刻共享的。也就是说,对任意时刻t,![]() 到
到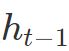 以及
以及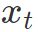 到
到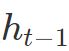 的网络参数都是相同的。
的网络参数都是相同的。
共享参数的思想和和卷积神经网络(CNN)是相通的,CNN在二维数据的空间位置之间共享卷积核参数,而RNN则是在序列数据的时刻之间共享参数。共享参数使得模型的复杂度大大减少,并使RNN可以适应任意长度的序列,带来了更好的可推广性。
双向RNN
单向RNN的问题在于t时刻进行分类的时候只能利用tt时刻之前的信息, 但是在t时刻进行分类的时候可能也需要利用未来时刻的信息。双向RNN(bi-directional RNN)模型正是为了解决这个问题, 双向RNN在任意时刻tt都保持两个隐藏层,一个隐藏层用于从左往右的信息传播记作, 另一个隐藏层用于从右往左的信息传播记作。
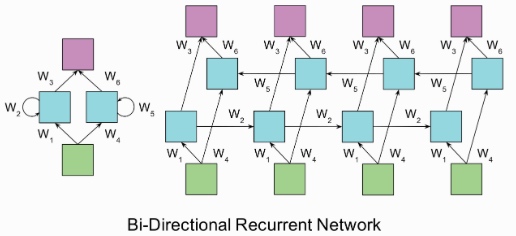
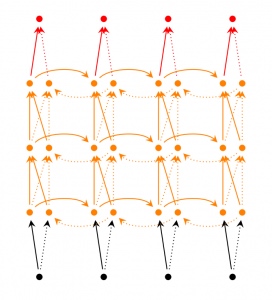
Deep(Bidirectional)RNNs与Bidirectional RNNs相似,只是对于每一步的输入有多层网络。这样,该网络便有更强大的表达与学习能力,但是复杂性也提高了,同时需要更多的训练数据。
Gradient Vanishing Exploding (梯度消失和梯度爆炸)
RNN训练困难的主要原因在于隐藏层参数w的传播:由于误差传播在展开后的RNN上,无论在前向传播过程还是在反向传播过程中w都会乘上多次,这就导致:
梯度消失:如果梯度很小的话(<1),乘上多次指数级下降,对输出几乎就没有影响了
梯度爆炸:反过来,如果梯度很大的话,乘上多次指数级增加,又导致了梯度爆炸
这个问题其实存在于任何深度神经网络中,只是由于RNN的递归结构导致其尤其明显。
对于梯度爆炸问题,可以通过截断的方式来有效避免:

而对梯度消失问题,则有很多不同的方案:
有效初始化+ReLU激活函数能够得到较好效果
算法上的优化,例如截断的BPTT算法。
模型上的改进,例如LSTM、GRU单元都可以有效解决长期依赖问题。
在BPTT算法中加入skip connection,此时误差可以间歇的向前传播。
加入一些Leaky Units,思路类似于skip connection
LSTM 全称叫 Long Short-Term Memory networks,它和传统 RNN 唯一的不同就在与其中的神经元(感知机)的构造不同。传统的 RNN 每个神经元和一般神经网络的感知机没啥区别,但在 LSTM 中,每个神经元是一个“记忆细胞”(元胞状态,Cell State),将以前的信息连接到当前的任务中来。每个LSTM细胞里面都包含:
输入门(input gate): 一个Sigmoid层,观察
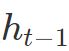 和
和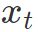 ,对于元胞状态
,对于元胞状态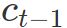 中的每一个元素,输出一个0~1之间的数。1表示“完全保留该信息”,0表示“完全丢弃该信息”:
中的每一个元素,输出一个0~1之间的数。1表示“完全保留该信息”,0表示“完全丢弃该信息”:
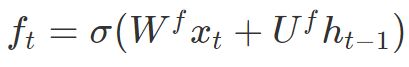
遗忘门(forget gate): 一个Sigmoid层决定我们要更新哪些信息,并由一个tanh层创造了一个新的候选值(结果在(-1, 1)(−1,1)范围)
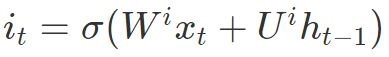
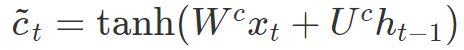
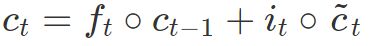
输出门(output gate):控制哪些信息需要输出
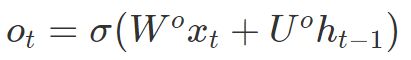
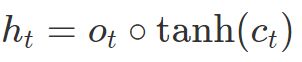
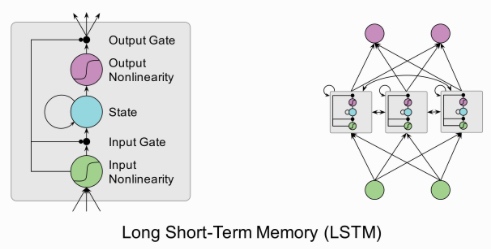
典型的工作流为:在“输入门”中,根据当前的数据流来控制接受细胞记忆的影响;接着,在 “遗忘门”里,更新这个细胞的记忆和数据流;然后在“输出门”里产生输出更新后的记忆和数据流。LSTM 模型的关键之一就在于这个“遗忘门”, 它能够控制训练时候梯度在这里的收敛性(从而避免了 RNN 中的梯度 vanishing/exploding 问题),同时也能够保持长期的记忆性。
如果我们把LSTM的forget gate全部置0(总是忘记之前的信息),input gate全部 置1,output gate全部置1(把cell state中的信息全部输出),这样LSTM就变成一个标准的RNN。
目前 LSTM 模型在实践中取得了非常好的效果, 只需要训练一个两三层的LSTM, 它就可以:
模仿保罗·格雷厄姆进行写作
生成维基百科的 markdown 页面
手写识别
写代码
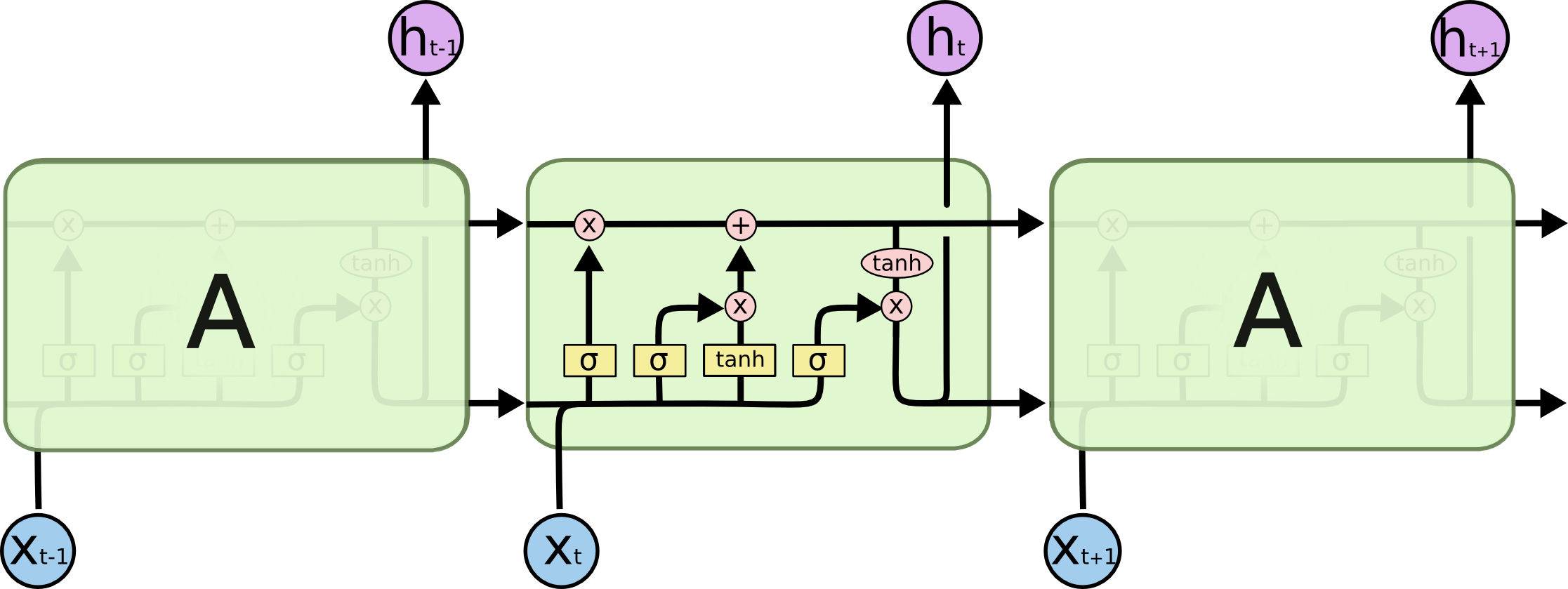
GRU (Gated Recurrent Unit) 是LSTM的变种,把LSTM中的遗忘门和输入门合并成为单一的“更新门(Update Gate)”,同时也将元胞状态(Cell State)和隐状态(Hidden State)合并,在计算当前时刻新信息的方法和LSTM有所不同。
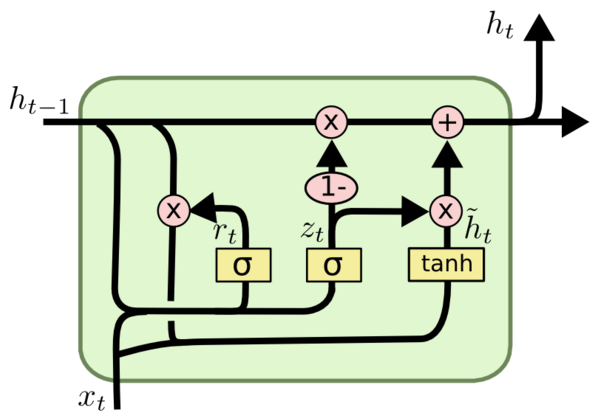
GRU与RNN对比:
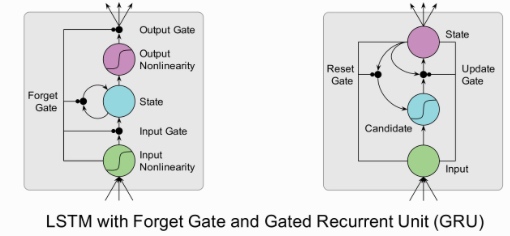
应用示例
import numpy as np |











